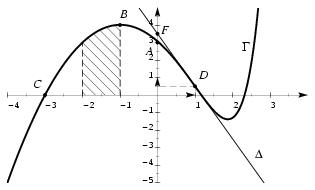
\exo {La courbe est donnée} \bgroup \sl Les buts de l'exercice sont~: \itemitem {--} la détermination de la fonction $f$, définie sur l'ensemble $\rset $ des nombres réels, dont la courbe représentative $\Gamma $ dans un repère orthogonal $(O, \vec \imath , \vec \jmath )$ est tracée ci-dessous (unité graphiques~: 2~cm en abscisse, 1~cm en ordonnée). \itemitem {--} le calcul de l'aire du domaine hachuré. \egroup \def \epspath {% $HOME/tex_doc/lycee/database/btsmai/analyse/equadiff/} On considère les quatres points $A (0, 3)$, $B (-1, 4)$, $C (-3, 0)$, $D (1\, ; 0, 5)$ de la courbe $\Gamma $, ainsi que la droite $\Delta $, tangente à $\Gamma $ au point $D$. La droite $\Delta $ passe par le point $F (0\, ;3, 5)$. $$ \superboxepsillustrate {equ2_019.ps} $$ \let \partie \llappartie \partie {A} % On cherche d'abord une fonction polynôme $g$, définie sur $\rset $ par $g (x) = ax^2 + bx + c$, où $a$, $b$ et $c$ sont trois nombres réels à déterminer pour que la courbe $P$ de $g$ passe par les points $A$, $B$ et $C$. \itemitemalphnum Montrer que la condition \og {\sl $C$ appartient à la courbe $P$}\fg \ conduit à l'équation~: $$ 9a-3b+c=0. $$ \itemitemalph En procédant de même pour $A$ et $B$, déterminer un système de trois équations à trois inconnues vérifié par $a$, $b$, $c$. \itemitemalph Résoudre ce système et vérifier que~: $$ g (x) = -x^2 -2x +3. $$ \itemnum On désigne par $g'$ la dérivée de $g$, et par $g''$ sa fonction dérivée seconde. \item {} Vérifier que, pour tout $x$ appartenant à $\rset $, $$ g'' (x) - 3g' (x) + 2g (x) = -2x^2 + 2x + 10. $$ \partie {B} % On admet que $f$, représentée par $\Gamma $, est une solution de l'équation différentielle $$ y'' - 3y' + 2y = -2x^2 + 2x + 10 \leqno (E) $$ dans laquelle $y$ est fonction de la variable $x$, définie et deux fois dérivable sur $\rset $. \itemitemalphnum Donner une solution particulière de $(E)$. \itemitemalph Résoudre l'équation différentielle~: $$ y'' -3y' +2y = 0. \leqno (E') $$ \itemitemalph Déterminer la solution générale de $(E)$. \itemnum Préciser, à l'aide des données initiales, les valeurs de $$ f (1) \qquad {\rm et} \qquad f' (1). $$ En déduire que, pour tout $x$ appartenant à $\rset $, $$ f (x) = -x^2 - 2x + 3 + {1\over 2} e^{2(x-1)}. $$ \itemnum Calculer l'aire, en $\cm ^2$, du domaine hachuré sur la figure, et défini par $-2\leq x \leq -1$ et $0\leq y \leq f (x)$. \item {} On donnera la valeur exacte de cette aire, puis sa valeur décimale arrondie au $\mm ^2$. \finexo \corrige {} \let \partie \llappartie \partie {A} \vskip -15pt \itemalphnum La condition \og {\sl le point $C$ appartient à la courbe $P$}\fg \ signifie que les coordonnées du point $C$ vérifient l'équation de la courbe $P$. L'équation de la courbe étant $y = g (x)$, on doit avoir $y_C = g (x_C)$. En utilisant les coordonnées $(-3, 0)$ dans l'équation $y = ax^2 + bx + c$ il vient alors \dresultat {9a-3b+c = 0}. \itemalph \alph \ En procédant de même avec les points $A$ et $B$, on obtient le système $$ \dresultat {\cases { c = 3 \cr a-b+c = 4 \cr 9a-3b+c = 0 \cr }} \qquad \Longleftrightarrow \qquad \cases { c = 3 \cr b = -2 \cr a = -1 \cr } \qquad {\rm soit} \qquad \dresultat {g (x) = -x^2 -2x+3} $$ \itemnum On a $g' (x) = -2x-2$ et $g'' (x) = -2$. On calcule alors $g'' -3g' + 2g$ pour trouver $-2x^2 + 2x + 10$. Ce qui prouve que la fonction $g$ vérifie \tresultat {$g'' -3g + 2g = -2x^2+2x+10$}. \partie {B} \vskip -17pt \itemalphnum On vient de voir que la fonction \tresultat {$g = -x^2-2x+3$ est une solution particulière de $(E)$} \itemalph On résoud maintenant l'équation sans second membre $(E')$. On considère l'équation ca\-rac\-té\-ris\-ti\-que associée $$ r^2 - 3r + 2 = 0. $$ Son discriminant est $\Delta = 1$, et cette équation admet les 2~racines réelles $r_1 = 1$ et $r_2 = 2$. On en conclut que la solution générale de l'équation sans second membre $(E')$ est \dresultat {y (x) = Ae^{2x} + Be^x} où $A$ et $B$ sont des constantes réelles arbitraires. \itemalph La solution générale de $(E)$ est alors \dresultat {y (x) = -x^2 -2x+3 + Ae^{2x} + Be^x} où $A$ et $B$ sont des constantes réelles arbitraires. \itemnum Sur le graphique, on voit que la courbe $\Gamma $ par passe $D (1\, ; 0,5)$. On en déduit que \dresultat {f (1) = 0, 5}. De plus, on lit que le coefficient directeur de la tangente en $D$ à la courbe est $-3$ (lorsque l'on avance de $x=1$, on avance de $y=-3$). On en déduit que \dresultat {f' (1) = -3}. \item {} On a $f (1) = Ae^2 + Be$. Et $f' (x) = -2x-2 + 2Ae^{2x} + Be^x$, d'où $f' (1) = -4 + 2Ae^2 + Be$. Ce qui donne $$ \matrix {\scriptstyle (1)\cr \scriptstyle (2)} \cases { Ae^2 + Be = 1/2 \cr 2Ae^2 + Be = -3 + 4 = 1 \cr } \quad \Longrightarrow \quad \matrix {\scriptstyle (2) - (1)\cr \scriptstyle (2)} \cases { Ae^2 = 1/2 \quad \Rightarrow \quad \mresultat {A = {1\over 2e^2} = {1\over 2} e^{-2}} \cr 2Ae^2 + Be = 1 \quad \Rightarrow \quad \mresultat {B = 0} \cr } $$ Donc la fonction $f$ cherchée est $$ f (x) = -x^2 -2x+3 + {1\over 2} e^{-2}e^{2x} \qquad {\rm soit} \qquad \dresultat {f (x) = -x^2 -2x+3 +{1\over 2} e^{2x-2}} $$ \itemnum Reste à calculer $$ I = \int _{-2}^{-1} -x^2 -2x+3 - {1\over 2} e^{2x-2} \, dx $$ Posons $u = 2x-2$. Alors $e^{2x-2}$ est de la forme ${1\over 2}u' e^u$, dont une primitive est ${1\over 2}e^u$. On en déduit le calcul de $I$~: $$ I = \left[ - {x^3\over 3} + x^2 + 3x - {1\over 2} \times {1\over 2} e^{2x-2}\right] _{-2}^{-1} = {11\over 3} + {1\over 4} \big( e^{-6} - e^{-4}\big) \approx 3,662 $$ Restera à multiplier le résultat par 2 puisque 1~unité d'aire vaut $2\times 1 \mm ^2$. \fincorrige