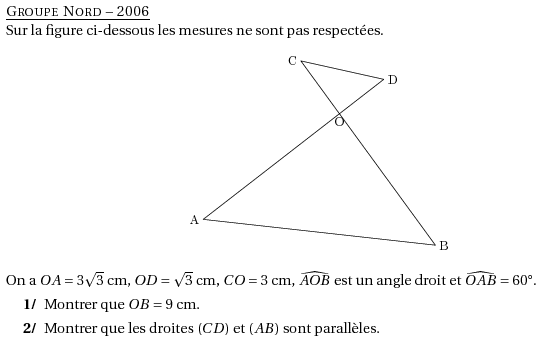
%@metapost:gpenord2006.mp %@Titre: Groupe Nord -- 2006 Sur la figure ci-dessous les mesures ne sont pas respectées. \[\includegraphics{gpenord2006.1}\] On a $OA=3\sqrt3$~cm, $OD=\sqrt3$~cm, $CO=3$~cm, $\widehat{AOB}$ est un angle droit et $\widehat{OAB}=60$\degres. \begin{myenumerate} \item Montrer que $OB=9$~cm. \item Montrer que les droites $(CD)$ et $(AB)$ sont parallèles. \end{myenumerate} %@Correction: \begin{myenumerate} \item \begin{multicols}{2} Dans le triangle $OAB$, rectangle en $O$, on a : \[\Eqalign{ \cos\widehat{OAB}&=\frac{OA}{AB}\cr \cos60&=\frac{3\sqrt3}{AB}\cr 0,5&=\frac{3sqrt3}{AB}\cr 0,5AB&=3\sqrt3\cr AB&=\frac{3\sqrt3}{0,5}\cr AB&=6\sqrt3~\mbox{cm}\cr }\] Dans le triangle $AOB$, rectangle en $O$, le théorème de Pythagore permet d'écrire : \[\Eqalign{ AB^2&=AO^2+OB^2\cr \left(6\sqrt3\right)^2&=\left(3\sqrt3\right)^2+OB^2\cr 36\times3&=9\times3+OB^2\cr 108&=27+OB^2\cr 108-27&=OB^2\cr 81&=OB^2\cr 9&=OB\cr }\] \end{multicols} \item Dans le triangle $OAB$, $D$ est un point de la droite $(OA)$ et $C$ est un point de la droite $(OB)$. \[\left. \begin{array}{l} \dfrac{OA}{OD}=\dfrac{3\sqrt3}{\sqrt3}=3\\ \\ \dfrac{OB}{OC}=\dfrac93=3\\ \end{array} \right\}\frac{OA}{OD}=\frac{OB}{OC}\] De plus, les points $A$, $O$ et $D$ sont alignés dans le même ordre que les points $B$, $O$ et $C$. Donc les droites $(AB)$ et $(CD)$ sont parallèles d'après la réciproque du théorème de Thalès. \end{myenumerate}