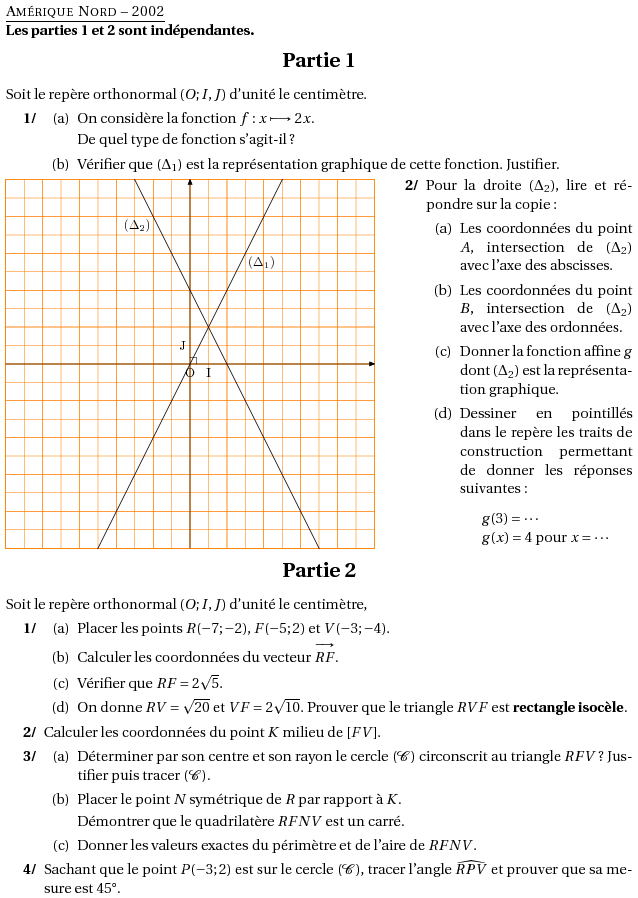
%@metapost:ameriquenord2002.mp %@Titre: Amérique Nord -- 2002 \textbf{Les parties 1 et 2 sont indépendantes.} \begin{center} \textbf{\Large{Partie 1}} \end{center} Soit le repère orthonormal $(O;I,J)$ d'unité le centimètre. \begin{myenumerate} \item \begin{enumerate} \item On considère la fonction $f : x \longmapsto 2x$. De quel type de fonction s'agit-il ? \item Vérifier que $(\Delta_1)$ est la représentation graphique de cette fonction. Justifier. \end{enumerate} \end{myenumerate} \par\compo{2}{ameriquenord2002}{1}{ \begin{myenumerate} \setcounter{enumi}{1} \item Pour la droite $(\Delta_2)$, lire et répondre sur la copie : \begin{enumerate} \item Les coordonnées du point $A$, intersection de $(\Delta_2)$ avec l'axe des abscisses. \item Les coordonnées du point $B$, intersection de $(\Delta_2)$ avec l'axe des ordonnées. \item Donner la fonction affine $g$ dont $(\Delta_2)$ est la représentation graphique. \item Dessiner en pointillés dans le repère les traits de construction permettant de donner les réponses suivantes : $$\begin{tabular}{l} $g(3)=\cdots$\\ $g(x)=4$ pour $x=\cdots$\\ \end{tabular} $$ %$$\includegraphics{ameriquenord2002.2}$$ \end{enumerate} \end{myenumerate} } \begin{center} \textbf{\Large{Partie 2}} \end{center} Soit le repère orthonormal $(O;I,J)$ d'unité le centimètre, \begin{myenumerate} \item \begin{enumerate} \item Placer les points $R(-7;-2)$, $F(-5;2)$ et $V(-3;-4)$. \item Calculer les coordonnées du vecteur $\vecteur{RF}$. \item Vérifier que $RF=2\sqrt5$. \item On donne $RV=\sqrt{20}$ et $VF=2\sqrt{10}$. Prouver que le triangle $RVF$ est \textbf{rectangle isocèle}. \end{enumerate} \item Calculer les coordonnées du point $K$ milieu de $[FV]$. \item \begin{enumerate} \item Déterminer par son centre et son rayon le cercle $\cal{(C)}$ circonscrit au triangle $RFV$ ? Justifier puis tracer $\cal{(C)}$. \item Placer le point $N$ symétrique de $R$ par rapport à $K$. Démontrer que le quadrilatère $RFNV$ est un carré. \item Donner les valeurs exactes du périmètre et de l'aire de $RFNV$. \end{enumerate} \item Sachant que le point $P(-3;2)$ est sur le cercle $\cal{(C)}$, tracer l'angle $\widehat{RPV}$ et prouver que sa mesure est 45\degres. \end{myenumerate}